Modelo general de funciones polinomiales
Las funciones polinómicas son, como su nombre lo dice, funciones que constan de un polinomio.
en donde n es un entero positivo, llamado, grado del polinomio. Resulta evidente, que el coeficiente del grado mayor, no puede ser cero, o sea, a tiene que ser diferente de cero, para que el grado del polinomio se n. Cualquiera de los otros coeficientes puede ser cero.
ejercicios:
1.-
- Suponiendo que la función que se nos presenta es de tercer grado, y sus intersecciones están en x = 2, x = -1 y en x = -3; la ecuación de la función es f(x) = (x-2)(x+1)(x+3)
- Debe quedar claro, que se tiene que conocer el grado de la función polinómica, ya que sin éste, las conclusiones que se puedan sacar pueden estas equivocadas.
Tenemos una función polinómica de grado 6, que sus intersecciones se encuentran en x = 1, x = 2, x = -1, x = 3, x = -2 y en x = 0; por lo tanto la función es:
f(x) = (x-1)(x-2)(x+1)(x-3)(x+2)(x)
Función polinomial de grado 1,2,3,4 y Representación gráfica
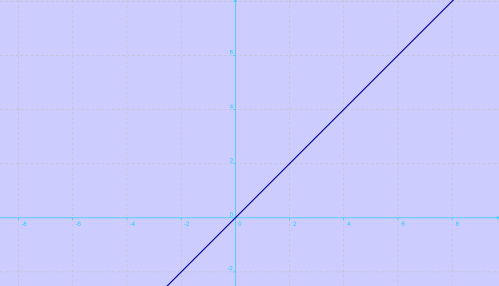
GRADO 1 tiene en su variable equis el exponente uno.La forma de esta función de grado uno es la ecuación de la línea recta, que tiene su gráfica como aparece de forma oblicua.
y = m x + b
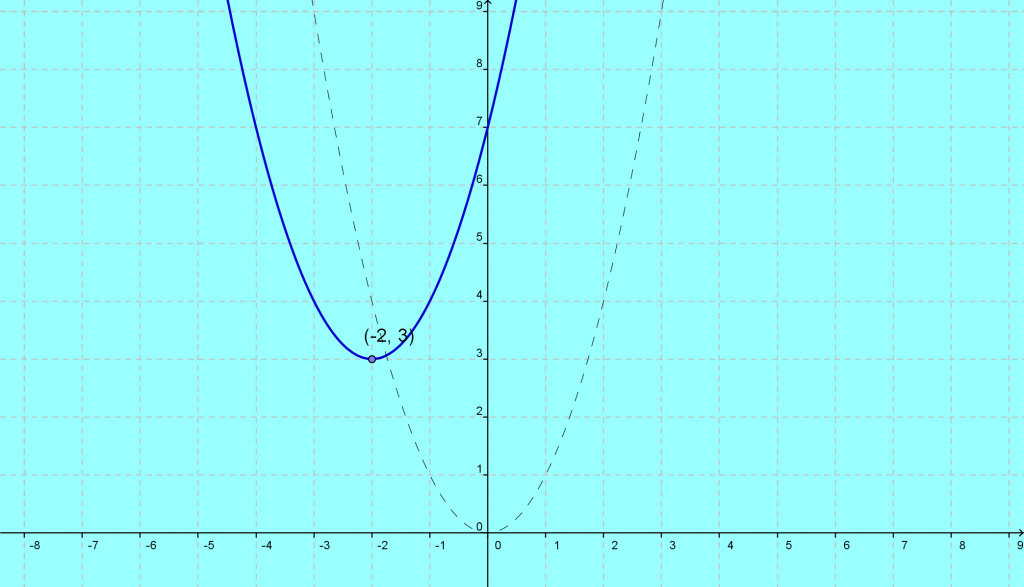
Y = ax2+ bx+ c que representa a una expresión cuadrática, donde a (distinto de 0), b y c son números reales.
GRADO 3 Se denomina función cúbica a toda función de la forma:
Su gráfica es una parábola.
GRADO 3 Se denomina función cúbica a toda función de la forma:
y= ax3 + bx2 + cx+ d; donde a (distinto de 0), b, c y d son números reales.





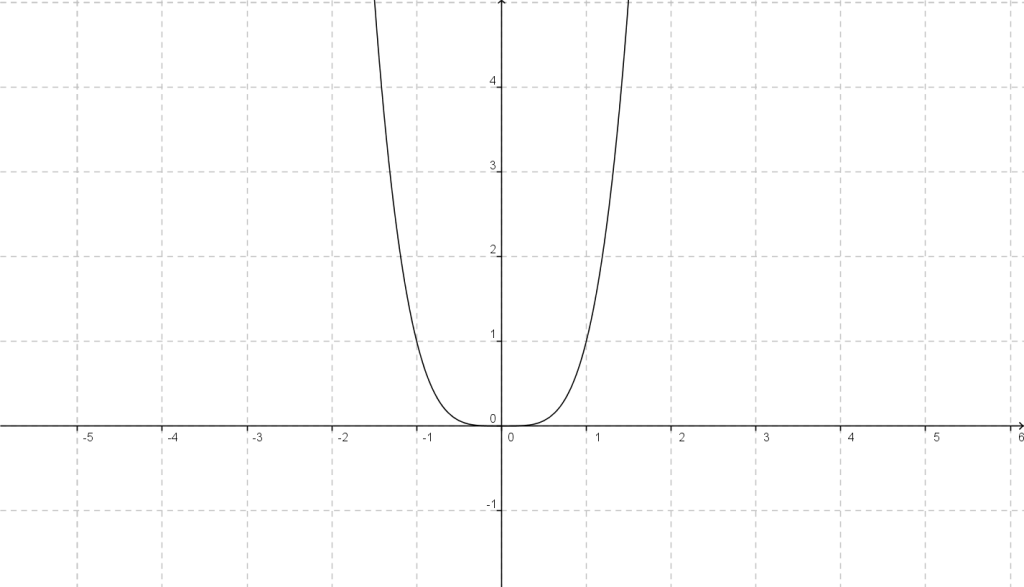
GRADO 4 Es la función de fórmula: y = ax4+ bx3+ cx2+ dx+ e; donde a (distinto de 0), b, c, d y e son números reales.
Características de funciones polinomiales grado cero, uno y dos
El grado de un polinomio está dado por el mayor exponente de la variable en el
polinomio, independientemente del orden en el que estén los términos, como se
muestra en las siguientes funciones:
1. f x = 7 Es de grado cero, se le conoce como función constante.
1. f x = 7 Es de grado cero, se le conoce como función constante.
2. f x = 4x-1 Es de grado uno, también conocida como función lineal.
3. 𝑓 𝑥 =x2 +5x+6 Es de grado dos, se le conoce como función
cuadrática.
4. 𝑓 𝑥 =4x2 +5x3 +1 Es de grado tres y se le conoce como función cúbica.
5. 𝑓 𝑥 =4x4 +3x3 +2x2+1Es de grado cuatro y se le conoce como función cuartica.
4. 𝑓 𝑥 =4x2 +5x3 +1 Es de grado tres y se le conoce como función cúbica.
5. 𝑓 𝑥 =4x4 +3x3 +2x2+1Es de grado cuatro y se le conoce como función cuartica.
Parámetros de las funciones de grados cero, uno y dos
La función constante, La función de grado cero es la que se conoce como
función constante, ésta es un caso particular de la función Polinomial y se inició
con ella en el primer bloque; su forma es:
𝑓 𝑥 = 𝑎, donde “a” es una constante
Su gráfica es una recta paralela al eje X y corta al eje Y en el punto (0, a).
Graficar la función 𝑓 𝑥 = 5, determinar su dominio y rango.
La función también se puede expresar como 𝑦 = 5, por lo tanto su gráfica es una recta horizontal a la altura de 5 .
𝑓 𝑥 = 𝑎, donde “a” es una constante
Su gráfica es una recta paralela al eje X y corta al eje Y en el punto (0, a).
- Ejercicio 1:
Graficar la función 𝑓 𝑥 = 5, determinar su dominio y rango.
La función también se puede expresar como 𝑦 = 5, por lo tanto su gráfica es una recta horizontal a la altura de 5 .
Dominio (−∞,∞), se debe recordar que el dominio de un polinomio siempre será
𝑅 = (−∞, ∞)
- Ejercicio 2:
Graficar la función 𝑔 𝑥 = − 72, determinar su domino y rango
La función constante puede ser cualquier número real, en este caso es un número racional, el cual equivale 𝑦 = −3.5, en la figura siguiente se muestra el resultado de la función.
La función constante puede ser cualquier número real, en este caso es un número racional, el cual equivale 𝑦 = −3.5, en la figura siguiente se muestra el resultado de la función.
Dominio (−∞, ∞)
Rango {7/2}
La función lineal. La ecuación lineal en su forma pendiente-ordenada en el origen
es:
𝑦 = 𝑚𝑥 + 𝑏
Donde m es la pendiente de la recta y b es la ordenada del origen. Vista como una función se representa de la siguiente manera:
𝑦 = 𝑚𝑥 + 𝑏
Donde m es la pendiente de la recta y b es la ordenada del origen. Vista como una función se representa de la siguiente manera:
𝑓(𝑥) = 𝑚𝑥 + 𝑏
𝑏.
Es la constante que indica el lugar donde la recta cruza el eje y, además
𝑏.
Es la constante que indica el lugar donde la recta cruza el eje y, además
Dónde:
se le denomina término independiente.
se le denomina término independiente.
𝑚. Es la pendiente de la recta, la cual está relacionada con su inclinación,
es el coeficiente de la variable.
𝑥. Es la variable independiente.
𝑥. Es la variable independiente.
- Ejercicio 3 :
𝑥 =2𝑥+3
𝑓 𝑥 =2𝑥+3
Dónde:
𝑚=2
𝑏=3
Existen métodos para graficar funciones lineales:
6. Sustitucióndevalores.
7. Intersección con los ejes coordenados. 8. Parámetros(𝑚y𝑏).
6. Sustitucióndevalores.
7. Intersección con los ejes coordenados. 8. Parámetros(𝑚y𝑏).
Cuando se tiene la regla de correspondencia de una función lineal es sencillo
trazar la gráfica, ubicando primero el punto que describe la ordenada en el origen
y a partir de él, mediante la pendiente, se ubica el segundo punto. 𝑥 =2𝑥+3
La función cuadrática. Las funciones cuadráticas se caracterizan por su grado 2,
éstas se expresan en su forma general como 𝑓 𝑥 = 𝑎𝑥2 + 𝑏𝑥 + 𝑐, con la
condición de que su coeficiente principal es diferente de cero (𝑎 ≠ 0) se compone
de la siguiente manera:
𝑎𝑥2. Término cuadrático. 𝑏𝑥. Término lineal.
c. Termino independiente.
Forma general de la función cuadrática. 𝑓 𝑥 = 𝑎𝑥2 + 𝑏𝑥 + 𝑐 Forma estándar de la función cuadrática.
𝑓 𝑥 = 𝑎(𝑥 − )2 + 𝑘
f(x) 𝑥 = 𝑥2 y 𝑔 𝑥 = 3(𝑥 − 2)2 − 4
𝑎𝑥2. Término cuadrático. 𝑏𝑥. Término lineal.
c. Termino independiente.
Forma general de la función cuadrática. 𝑓 𝑥 = 𝑎𝑥2 + 𝑏𝑥 + 𝑐 Forma estándar de la función cuadrática.
𝑓 𝑥 = 𝑎(𝑥 − )2 + 𝑘
f(x) 𝑥 = 𝑥2 y 𝑔 𝑥 = 3(𝑥 − 2)2 − 4
Solución. Al tomar los valores quedan de la siguiente manera. a)𝑓𝑥 =𝑥2.
- Ejercicios 5:


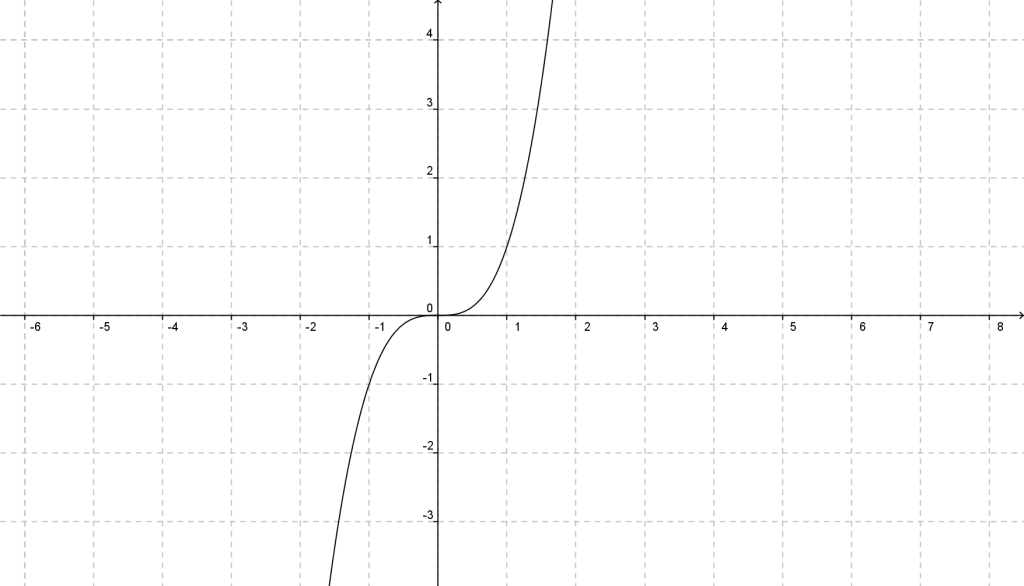
No hay comentarios:
Publicar un comentario